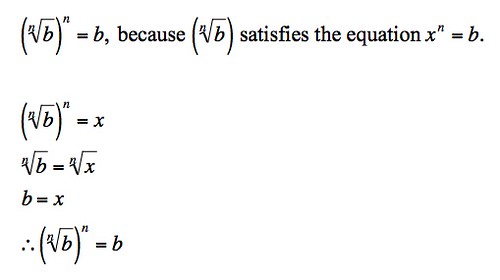
I don't follow Dolciani's statement at the top.
At all.
update 5.29.2009
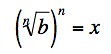
This equation doesn't follow from Dolciani's equation; I wrote it to see whether I would understand Dolciani's statement once I solved it.
Of course, I don't know whether I solved it. It seems to me I've got a problem with cases in which the exponent is an even number - ?
The series of equations underneath the top line are mine; I was trying to figure out why Dolciani's explanation is an explanation.
ReplyDeleteI may be reaching the point where I need a math teacher.
Maybe this will motivate me to check in with ALEKS again.
Seeing as how I've been paying for ALEKS all this time.
Are my series of equations wrong?
ReplyDeleteSeems to me that x could be either a positive or a negative number, depending on whether n is odd or even, in which case this doesn't work----
do you understand dolciani's first statement?
ReplyDeleteThe nth root of b is a value for x that yields a true equation, as the nth power of the nth root of b is b.
your second statement is wrong. it's not the nth root of b to the nth power is x. it's the nth root of b is x.
so your next statement is wrong, and the rest are wrong too.
the nth root of b = x.
raise both sides to the nth power.
that leaves b = x^n.
There are n solutions to the polynomial x^n = b. One of them is the (positive) nth root of b.
does this help?
solution to x-to-the-n is b.
ignore the gibberish after "does this help?"
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteOne thing that is confusing about the line you quote is that it is basically of this form:
ReplyDelete"a certain statement" because "a rewording of the same statement"
whereas you would expect, given the word "because", something like
"a certain statement" because "a reason for it".
Just remember that the radical notation simply means, in this case, "an nth root of b" (typically the positive real nth root if there is one, such as when b is a positive real number and n is even), and the equation x^n = b defines the nth roots of b.
your second statement is wrong. it's not the nth root of b to the nth power is x.That can't be wrong, can it?
ReplyDeleteI wrote that simply as an equation to be solved. It doesn't relate the Dolciani's statement.
????
There is a problem with stating
ReplyDeletes = t => nth root of s = nth root of t
in that s and t have n nth roots, so is the nth root extracted on the left the same nth root extracted on the right?
A better way to think of this, to understand the original Dolciani statement, is not to try to solve an equation, but to realize that the Dolciani statement is essentially the definition of what one means by nth root.
An nth root of b is a number such that if you raise it to the power n you get b.
I'm going to print these explanations out and study them.
ReplyDeleteI have this experience with Dolciani pretty often.
She'll write a short, precise (seems precise to me) 'explanation' and suddenly a concept that seemed obvious seems inexplicable.
I assume that's because I'm trying to teach myself using a textbook that is meant to be used with a math teacher ---- ?
"a certain statement" because "a rewording of the same statement"
ReplyDeletewhereas you would expect, given the word "because", something like
"a certain statement" because "a reason for it".Yes, this is my problem.
When I read the word 'because' I absolutely think I've been given a reason, not a restatement of the original statement.
Even though a restatement of the original statement is often a good way to explain something, one I often use myself.
Apparently I don't understand math well enough to recognize restatements as restatements.
Although....I'm pretty sure I wouldn't use the word "because" when I am restating a claim....
I dropped an update into the original post, fyi
ReplyDeleteI think it's a way of being true (rigorous) without scaring away people who don't know about imaginary numbers.
ReplyDeleteDolciani can't bear to teach anyone that the "nth root" function is the inverse of the "nth power" function, so she just asserts the nth root of b (if it exists in the real numbers) is AN answer because it satisfies the equation (x^n = b).
This way, she doesn't have to get involved in complex trig, or have to explain multiple roots; just stick with whole number powers and roots and mind those even and odd powers.
--rocky
Saxon Math teaches imaginary numbers in Algebra 2.
ReplyDeletedo you understand dolciani's first statement?I do -- that's what threw me for a loop.
ReplyDeleteAs I was saying, this happens pretty often for me, trying to teach myself using Dolciani.
I'll understand something - or be completely familiar with it & able to use it - and then she'll add a "because x,y,z" phrase & I'll have no idea what she's talking about.
I've had a problem following her proofs, too.
I need proofs in which EVERY SINGLE STEP is spelled out, not assumed.
I'm starting to be able to understand that certain steps will always be omitted ---
Hi, I'm your math teacher.
ReplyDeleteGood thinking to recognize that even and odd n's are different. There's another subtlety here though. I think you understand the case where n is odd, so I'm going to do an explanation of what happens when n is even.
Not: I'm using b^1/n for the nth root of b because I'm not as spiffy with my HTML as you are.
I also want to clear up a definition thing, right at the start, and that is, if you are working with real numbers only (probably that's the case with what you are working on now), then b^1/n does not mean all of the n-th roots, it means the principal n-th root, which, if n is even and b is positive is the positive nth root.
One thing that might be confusing you is that in the related expression (b^n)^1/n, then if b is negative, (b^n) is positive, and so it has a positive nth root, and, in the usual case (where you are working only with real numbers) (b^n)^1/n = |b| because b^1/n is defined to be the positive nth root (so, if b is positive, then it equals b, and if b is negative, you get the positive instead of the negative).
But! That isn't the statement. You have here (b^1/n)^n. If you are working with real numbers only, then if b is negative (n even), then b^1/n doesn't exist, and so the whole equation goes poof (you couldn't have a b^1/n, so you can't write the equation, and this is a case that doesn't count because it doesn't exist). If b is positive, then b^1/n is still defined to be the positive square root, and (b^1/n)^n=b
Now, my explanation above is only the right explanation if you are working only with real numbers. If you are allowing complex numbers (so you can have a sqrt(-1)), then the explanation changes: now, b^1/n is not the principal (positive) n-th root, it is (depending on how you define it) either a randomly chosen one of the n complex n-th roots, or it is the set of all n of the complex n-th roots. However, if you pick any of the n complex n-th roots, and you do (b^1/n)^n=(randomly chosen n-th root of b)^n=b. So the n-th power of an n-th root is always b, no matter which n-th root it was.
if you are working with real numbers only (probably that's the case with what you are working on now), then b^1/n does not mean all of the n-th roots, it means the principal n-th root, which, if n is even and b is positive is the positive nth root.right - and that's another source of confusion for me, working on my own with Dolciani. She explains the principle square root but then says that for certain square roots you need to specify absolute value.
ReplyDeleteI'm not following whn I need to include thee absolute value notation & when I don't.
(Will read your comment now!)