Saturday, December 5, 2009
letter to the editor, part 2
To the editor:
On November 24 I attended a school board meeting at which Renay Sadis, principal of Dows Lane Elementary School,* gave a presentation she had rehearsed before superintendent Kathleen Matusiak earlier in the week.
Ms. Sadis’ report to the board did not mention student achievement. Focused entirely on “new initiatives” at the school, Ms. Sadis’ remarks were so empty of substance that one board member called her presentation a “commercial.”
During the time allotted to the audience for questions and comments, I asked the following questions:
How many remedial reading teachers does Dows Lane have on staff?
Answer: 3
How many general education students need remedial reading instruction?
Answer: Ms. Sadis did not know.
How many special education students - students with Individualized Education Plans - are enrolled in Dows Lane?
Answer: Ms. Sadis did not know.
How many of our students would score “Advanced” in reading on the National Assessment of Educational Progress (NAEP), the federal test known as “The Nation’s Report Card”?
Answer: Ms. Sadis had not heard of NAEP.
Finally, and most importantly, what are our plans to reduce the number of students who need remedial reading instruction?
Ms. Sadis, who last year commanded a salary of $165,000, had no answer.
I’d like to suggest that, going forward, the district consider recruiting teachers and administrators who have worked in successful charter schools here or in states where charter schools have been founded to teach high-SES student populations. A charter school is simply a public school with accountability and a tight budget; no one who has worked in a charter school would show up at a school board meeting not knowing how many struggling readers are in her school.
Educators who have come up through the ranks of the charter school movement have a different philosophy from those who, like Ms. Sadis and Superintendent Matusiak, have worked exclusively in traditional public schools. Where traditional public schools focus on compliance with state and federal mandates, charter school teachers and administrators concentrate on performance. Charter school educators are committed to the success of the individual child.
That is for the long-term, of course. In the short-term, I would like to suggest that the Board require administrators to devote themselves — and their presentations — to student achievement.
Catherine Johnson
The Rivertowns Enterprise
Friday, December 4, 2009
p 21
* enrollment: 493; district per pupil spending: $28,291.
Friday, December 4, 2009
Teaching How Science Works, by Steven Novella MD at Neurologica Blog
Another way in which a good sounding idea for science education has been poorly executed on average is the introduction of hands-on science. Ideas are supposed to be learned through doing experiments. However, textbook quality is generally quite low, and when executed by the average science teacher the experiments become mindless tasks, rather than learning experiences.
I have two daughters going through public school education in a relatively wealthy county in CT (so a better than average school system) and I have not been impressed one bit with the science education they are getting. Here is an example – recently my elder daughter had to conduct an experiment on lifesavers. OK, this is a bit silly, but I have no problem using a common object as the subject of the experiment, as long as the process is educational. The students had to test various aspects of the lifesavers – for example, does the color affect the time it takes to dissolve in water.
The execution of this “experiment” was simply pointless. They performed a single trial, with a single data point on each color, and obtained worthless results that could not reasonably confirm or deny any hypothesis. By my personal assessment, my daughter learned absolutely nothing from this exercise, and afterwards complained that she was becoming bored with science.
Thursday, December 3, 2009
Evidence in Education
Nonjudgmental arenas for discovery
"At Montessori, we believe dentistry is more than just the medical practice of treating tooth and gum disorders," school director Dr. Howard Bundt told reporters Tuesday. "It's about fostering creativity. It's about promoting self-expression and individuality. It's about looking at a decayed and rotten nerve pulp and drawing your own unique conclusions."
"In fact, here at Montessori, dentistry is whatever our students want it to be," Bundt continued.
If you feel yourself getting ill, just remember, the article is satire. It's supposed to be humorous.
Wednesday, December 2, 2009
Precision Teaching In A Fuzzy World
Anyway, I've struggled with why such a common sense, obvious truth (precision measurement and teaching) seems to hit such disproportionate resistance to any such implementation by the education establishment. I'm so old that I have all sorts of ancient oblique anecdotes to sift through, and as I sifted through my old warehouse of stories, it hit me. I've been through this exact scenario before. I just never recognized the connection.
In the late seventies I was a test engineer for a computer company. In those days testing was pretty much an end of the line event. Hundreds of people built stuff, then threw it over the wall to a test system that found defectives and fixed them before shipping to customers. I'm over simplifying of course because there were always interim tests of subunits, but the important point to this discussion is that testing was, culturally at least, a post manufacturing event. Defects were intentionally passed on to others to resolve.
As products grew more sophisticated it became more and more difficult to build a high percentage of good units on your first try and the hypocrisy of passing on defectives became a problem. Eventually, most of what was built in its first pass was in fact bad. Simple probability worked against us as circuits went from tens of thousands of components to tens of millions of components. The cost of test machines skyrocketed to over ten million dollars a copy and the programming costs to bring one of these beasts on line soared along with the purchase price. A point was reached where it was physically impossible to test-in goodness as a post build event.
The forces of stasis in this culture were huge. Entire buildings had been erected to sustain this post test culture but in private enterprise stress causes change. You change or die without a monopoly position. In order to address this increasing complexity, testing evolved from a post build culture to one that was integrated into manufacturing. Instead of testing products after they were assembled you tested people, parts, machines, and processes before and during the process of putting them together. We found that if you perfected the front end you didn't have to test on the back end (as much) and ultimately some products had such high yields that if they were found (at some final system check) to be bad, this was such an infrequent event that it was economically unsound to fix them. Test engineering went from 'find and fix' to 'find and prevent'. This was an enormous paradigm shift that took a decade to complete.
In education we have a very analogous paradigm shift to work through if we want to get to precision teaching.
Today, we have a 'post build' culture. Kids are tested after being 'built' to see if they've gotten it or not. Where this process gets dicey is when it bumps up against the physical infrastructure of the ordinary school. Schools are a collection of rooms. There are 1st grade rooms and 2nd grade rooms and on and on. There are 1st grade teachers and 2nd grade teachers. There are 1st grade students and 2nd grade students. You get the idea. The infrastructure is entirely designed as a sequential set of processes in an assembly line with the kids passing though the system like little computer parts .
Once you understand this locked in, sequential infrastructure it's easy to see why you can't teach with precision. Teaching with precision creates 'rejects'. It creates students with identified deficiencies that need to be fixed. The most effective (for the status quo) testing system in this infrastructure is one that leaves deficiencies in a fuzzier state, otherwise how can you justify passing the 'part' down the line to the next assembly station. Only fuzzy measurement can possibly support this sequential structure. This is exactly like the old computer manufacturing. It knowingly passed defects down the line to the next step in the process. In this culture you don't hang a sign on the defective parts telling the world you just built junk. You just don't mention it.
Precision teaching would blow up this infrastructure!
Precision teaching tests to find out what to do next, not to produce a grade. So if you want to measure and teach with precision, the implication is that you must also build an infrastructure that is responsive to what you learn in your measurement. To navigate a paradigm shift from today's post test culture to a pre test culture, a culture where testing is designed as a prerequisite screen for 'the next step', the infrastructure has to have components equipped with a finer edge than the blunt sword of grade levels, teachers in rooms, and monolithic curricula.
The challenge for precision teaching is to devise an infrastructure to support it. If you do the testing right and uncover lots of little defects that need to be remedied before passing on the 'parts', then you need a structure that has a great variety of paths that can accommodate what you uncover with your precision. Instead of a sequential set of processes you need a web of processes that can provide for all the twists and turns that are the inevitable detritus of human interactions.
I'm convinced that precision teaching can not happen without fundamental change to the infrastructure and it is fear of this fundamental change which creates the illogical resistance to precision measurement and thus precision teaching . It's far easier to pretend that Johnny can add and pass him on, than to prove he can't and then have to do something about it.
"Practical Differentiation Strategies in Math"
It was a dinner-and-talk event. Several schools sent several teachers, and occasionally an administrator, to socialize and the listen to a 90 minute presentation. There were somewhere around 3 dozen people in attendance.
The talk was given by Liz Stamson, a math specialist with Math Solutions. You can see a related set of slides for a talk by her here. Those slides are for the webinar at this link to differentiation.
Stamson's talk was more specifically geared to engaging the math teachers. She spent most of her time talking about creating lesson plans and assignments that met the goals of differentiated instruction.
Stamson's talk assumed the full-inclusion classroom. She began the talk by saying that teachers were already needing to address students that could have vastly different "entry points" into the math curriculum. No mention was made of whether this was good or bad, whether grouping by ability was a help or hindrance. Full inclusion was a fact for teachers, not a point of argument.
Given that, she said, differentiation (that was the phrase, not differentiated instruction) was a way to help teachers engage all of their students. She stressed that differentiation could occur in content, process, and product. Her main ideas in how to differentiate content were to create "open tasks": questions that didn't have set answers, but had a multitude of answers. For example:
"what is the perimeter of a rectangle with length 10 and width 3", is a "closed" task. It has one answer. Such closed tasks, with one solution, and no critical thinking, does not lend itself to a differentiated classroom.
Instead, she promoted "open tasks" and "choice." What she meant by "open tasks" were problems that don't have one answer. By "choice" she meant allow the students to choose which problems on a problem set they must do. For example, instead of asking the above perimeter question, one could ask "describe a rectangle whose perimeter is 20." Such a task "opens" the problem to more creative thinking, allowing the more advanced students to find their own solutions (or to find a set of solutions), while still allowing the minimally skilled students to contribute. She said she'd offered the following "assignment" to her students, she said : "Do all the problems whose answers are even." This promotes critical thinking, she said, as they must investigate all of the problems to learn which ones fit the criteria.
She illustrated an open task with the "Which Does Not Belong" problem.
She gave the following sets:
2, 5, 6, 10
9, 16, 25, 43
cat, hat, bat, that
She asked the teachers to "work" the following problems. Teachers were seated together by grade (rather than by school), and were asked to collaborate. For each set, remove one item. Find a rule by which all of the remaining elements belong to the set, but the removed one does not. Repeat for all items.
The teachers gave a variety of answers.
Someone said that with the 2 removed, the remaining numbers' words were in alphabetical order. One said that with the 5 removed, the remaining numbers could all be written by 3 letter words. Another said all the remaining numbers were even. With the 10 removed, the remaining numbers were single digits said someone. With the 6 removed, the numbers formed a set of divisors of 10 (or alternately formed the number sentence 2 * 5 = 10.)
Ms. Stamson used this variety of answers to illustrate her point: all answers were valuable, no one had to get the "wrong" answer, even if some students didn't see immediately what the others did. This was practical differentiation--the more complicated patterns were found by the more advanced students, the less in depth by the students with less skills, but all could satisfy the assignment. The later grades could use factors, fractions, or other mathematical terms more appropriate to their lessons, while the younger grades could do this assignment with words or pictures if necessary.
She encouraged the teachers to create their own sets during this talk, stopping for several minutes.
Differentiation of process and product seemed to mean giving out different problems/homework/quizzes to different children. She advocated designing assessments/quizzes with several problems whose values were weighted, and requiring the student to complete a certain total value of problems, but allowing the students to pick which to do. The simplest problems were worth 1 point, say, and the hardest 10, and 15 points were needed for completion of the assignment. She suggested that such choice allowed all student to build confidence. She said also that it allowed a teacher to be "surprised" by a student who did difficult problems when the teacher expected to only do the easiest problems (as well as surprised when a good student did only the easiest). She also offered that the best students would challenge themselves and do all of the problems, so this provided a way to meet their needs for more or harder work.
When a teacher asked whether such choices were really practical, she admitted that such assignments might not be practical for daily practice, but suggested simply offering different students different problems. "Do you actually suggest assigning different problems to each student?" one teacher asked. Yes, she said: just hand out a worksheet, and highlight problems 3,4, and 7 for one child, and 1, 8, 9 for another. "If the culture of your classroom celebrates differences, then it's natural. We are all different, so of course we all have different strengths, and we all do different practice problems."
I could not tell from my vantage point, seated with a few lower grade teachers, if the room generally viewed the talk favorably. I assume the answer was yes, as who would attend such an evening if they were not already so inclined? The teachers at my table were quite dutiful at doing her assignments to us during dinner, and took very seriously everything she was saying. There were few questions from the audience, though. I couldn't tell, but perhaps that's just the style of talk, or the general behavior of a Minnesotan audience.
What is new with the science on math disabilities?
Wednesday, December 02, 2009
Atypical numerical cognition, dyscalculia, math LD: Special issue of Cognitive Development
A special issue of the journal Cognitive Development spotlights state-of-the-art research in atypical development of numerical cognition, dyscalculia, and/or math learning disabilities.Article titles and abstracts are available at Kevin McGrew's excellent IQ's Corner blog.
-----------
Joe Elliot on dyslexia:
"Contrary to claims of ‘miracle cures’, there is no sound, widely-accepted body of scientific work that has shown that there exists any particular teaching approach more appropriate for ‘dyslexic’ children than for other poor readers."
I am in agreement with Elliot.
I wonder if the same will be found to be true for dyscalculia and kids who struggle with math.
Tuesday, December 1, 2009
"deep shift in the makeup of unions"
A study has found that just one in 10 union members is in manufacturing, while women account for more than 45 percent of the unionized work force.
The study, by the Center for Economic Policy Research, a Washington-based group, found that union membership is far less blue-collar and factory-based than in labor’s heyday, when the United Automobile Workers and the United Steelworkers dominated.
[snip]
About 48.9 percent of union members are in the public sector, up from 34 percent in 1983. About 61 percent of unionized women are in the public sector, compared to 38 percent for men.
[snip]
The study found that 38 percent of union members had a four-year college degree or more, up from 20 percent in 1983. Just under half of female union members (49.4 percent) have at least a four-year degree, compared with 27.7 percent for male union members.
[snip]
The percentage of men in unions has dropped sharply, to 14.5 percent in 2008, from 27.7 percent in 1983, while the percentage for women dropped more slowly, to 13 percent last year, from 18 percent in 1983. For the work force over all, the percentage of workers in unions dropped to 12.4 percent last year, from 20.1 percent in 1983.
Economix: Union Members Getting More Educated
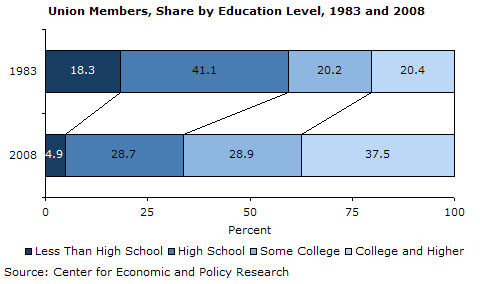
The 2002 Census shows that "more than one-quarter" of adults hold a college degree.
Amongst union members, that figure is 37.5%.
Monday, November 30, 2009
Do You Only Get What You Measure
I attended an interesting faculty meeting today. These are once a month affairs where we are tasked to work on a continuing project. The current project was for each grade level team to analyze our state test data and report out on any significant findings along with ideas on what we might do to mitigate any adverse findings.
Math was the first topic. Turns out (no surprise here, we've been doing this since the seas parted) number sense is a big deal. It's the highest percentage test item and also where we do the poorest.
When the elementary teachers made their presentations they described their efforts in this very area of arithmetical calculation, number sense stuff. Since I'm pretty frustrated with my kids' lack of ability in this domain, my ears were perked. They work really hard on this. I know this from personal observation. But, there was one omission.
Someone asked how many kids leave third grade knowing how to add. Crickets! It's not measured.
I posed a question about what is meant by 'knowing how to add'. Crickets! There is no criteria.
Then I was asked what I meant by asking that. My response had to do with objective measurement vs. subjective measurement. Crickets! Nobody has objective measures.
Here's what the consensus answer was (I'm paraphrasing). "We have a pretty good idea what most of our kids can do when they leave us." There you have the big omission. We have a completely fuzzy string of descriptors all wrapped up in one sentence; pretty good, most of, and can do. Not only is there no objective measurement taking place, there isn't even an awareness of what one should look like.
Suddenly the scales dropped from the eyes of this grasshopper. We're getting what we measure! Subjective measures lead to subjective results. We aren't asking for kids to know facts. We're asking kids to get answers and it's perfectly OK if they do this with fingers, toes, and mystical incantations to math gods. We even meet the, by God, state standards with this fuzz as they ask for no more.
I'm of the school that says if you can't measure it then it doesn't exist. Have we reached a point that it is culturally unacceptable to do anything that isn't fuzzy? Am I working in a measurement resistant culture? To me, with my background, uncovering fuzziness is just an indicator that I need to do more work to expunge the fuzz. To my colleagues it seems like fuzziness is not a clue, it's an objective.
Please, just disabuse me of this if you think I've just had too much coffee, but I think it would be really interesting to find out if there has ever been a correlation study in education to see if it's true that "You get what you measure." From this anecdote it sure seems to have some truth to it.





