
I've been cruising The Corruption of the Curriculum [Fordham Foundation link] for awhile now.
Just snapped up a copy for five bucks at Amazon.
They do what they do.
Thinking about schools and peers and parent-child attachments....I came across one of my favorite posts .


"We were told to cross off the kids who would never pass. We were told to cross off the kids who, if we handed them the test tomorrow, they would pass. And then the kids who were left over, those were the kids we were supposed to focus on."
source:
Is NCLB Leaving Children Behind?
via: Fordham Foundation
1 mile = 5280 feet = 1760 yards = 8 furlongs = 320 rods.
Unless it's a nautical mile, which is 1852 meters (precisely), 6076.115 ft, or quite close to 1 minute of longitude at the equator (its original definition).
The most important thing to know about transfer of learning is that it cannot be assumed (Mayer & Wittrock, 1996). Just because a student has mastered a skill or concept in one setting or circumstance, there is no guarantee whatsoever that the student will be able to apply this skill or concept to a new setting, even if the setting seems (at least to the teacher) to be very similar (Mayer & Wittrock, 1996)….Lave (1988)* describes a man in a weight-loss program who was faced with the problem of measuring out a serving of cottage cheese that was three-quarters of the usual two-thirds cup allowance. The man, who had passed college calculus, measured out two-thirds of a cup of cottage cheese, dumped it out in a circle on a cutting board, marked a cross on it, and scooped away one quadrant. It never occurred to him to multiply 2/3 x 3/4 = 1/2, an operation that almost any sixth-grader could do on paper (but few could apply in a practical situation).
p. 229
I was told once by the principal of an elementary school in a very affluent town: "There's nothing we're doing at our school that can top what these kids get at home in their background. We could not teach them a thing in third grade, and at the end of year they'd still score above grade level."
Today, schools are rated poorly if their students do not score well on state-mandated tests, regardless of whether children’s learning has been helped or hindered by the school environment. By the same token, schools serving affluent families in a resource-rich community are assumed to be good schools on the basis of children’s higher test scores, which may be high even in the face of a mediocre education. Downey and his colleagues [17, 34] have developed a new approach to measuring school performance that accounts for seasonal differences in learning, wherein the portion of student performance that can be attributed to the school is separated from the portion due to nonschool learning periods, including both during the period before a child enters school and over the summers as they progress through school. Using data from the Early Childhood Longitudinal Study (ECLS), they find striking differences in school impact with this approach:
[O]ur analyses of reading suggest that 70 percent of currently labeled “failing” schools are not really failing…Many teachers and administrators working in schools serving disadvantaged children face a variety of challenges including scarce resources, large classes, and little parent involvement. Despite these conditions, a surprising number of professionals serving disadvantaged students appear to be doing a good job, much better than previously thought.
[17 p. 24]
Using this measure of “school impact,” in recent analyses of data from the Early Childhood Longitudinal Study (ECLS), the researchers find that many schools considered “failing”—due to the low test performance of their students—are actually doing a better job of education than schools with much-higher-performing students.
from The Learning Season: (pdf file)
The phenomenon of summer undoing school-year learning has come to be known as
“summer learning loss.” It was first commented on in 1906 [29], followed some decades later by the 1978 book Summer Learning and the Effects of Schooling, by Barbara Heyns, which was based on her study of New Jersey students. More recently, a number of researchers [17, 30–37] have found that nearly all the differences in achievement between poor and middleclass children can be attributed to changes in learning that take place over class the summer. This finding is particularly surprising—and important—given that the vast majority of public and philanthropic resources are dedicated to school-year education, and that relatively scant resources are earmarked for summer programs.
While summer learning loss has operated mostly “under the radar,” the effects of early childhood experiences on racial, ethnic, and class test-score achievement gaps have received a great deal of media and research attention. Evidence from a set of longitudinal studies demonstrating that preschool children benefit significantly—and permanently—from early learning experiences [10–12], along with new understandings from neuroscience [4, 38], has formed the foundation for a national movement: public preschool is fast becoming a norm across the country, and public funding for early-childhood care and education is growing.
Despite these growing gaps, research on seasonal learning shows that children in all socioeconomic groups are actually progressing at the same rate during the school year. Yet during the summer middle-class children generally continue to learn, or hold steady, especially in reading, while poor children lose knowledge and skills [42]. These findings are especially surprising, given the well-documented disparities in facilities, teacher quality, curriculum, safety, and materials between schools serving poor children and those in affluent communities [9, 43–46]. Research on seasonal learning demonstrates that even struggling schools provide some support for children’s learning, at least compared with a summer devoid of educational experiences [34, 36, 47].
Miller presents past research showing that, during the school year, low- and high-SES students make similar progress on standardized tests. Between spring and fall, however, the scores of low-SES students either level off or decline, while those of high-SES students continue to rise. Research by Alexander and colleagues confirms this trend. Tracking 325 Baltimore students, they found that high-SES students gained a cumulative 47 points on reading test scores during the summer, while their low-SES counterparts lost 2 points.
Miller quotes an NCES study, for instance, which found that "42.5 percent of children in high-income households attended camp the summer after kindergarten, compared with just 5.4 percent of children in low-income" families.
In the summer of 2003, filmmakers Bradley Beesley and Sarah Price joined forces to tackle a documentary subject of almost unbearably powerful emotions and compulsively watchable conflict: a season at a Midwestern sleepover camp.
[snip]
The film's two stars are Holly, a charismatically energetic and wistful girl, and Cameron, an overweight kid with an unusual flair for challenging counselors' patience and making enemies among his peers.
[snip]
Holly and Cameron "are our main characters because they related more to adults and adult-type issues and they didn't have a whole lot of friends within their cabins," Mr. Beesley said.
[snip]
Something else the filmmakers discovered was how much prescription medication has permeated children's lives. "There was this group of kids going to the nurse's office every night," Ms. Price said. "It took us a few days to catch on to what was going on." Per their parent's wishes, campers diagnosed with attention deficit disorder and other behavioral maladies were reporting to receive their prescribed meds. Images in "Summercamp!" of what appear to be perfectly healthy children lining up to swallow pills like the mental patients in "One Flew Over the Cuckcoo's Nest" are disturbing; at the same time, a scene in which one boy flirts with a girl by bragging about the magnitude of his ADD is hilarious.
[snip]
"Summercamp!" also doggedly follows Cameron down a road of trials littered with obstacles of the boy's own devising. Cameron has an unfortunate genius for clumsily rebellious behavior; witnessing his steady failures and occasional triumphs will likely empower the inner outcast in anyone. "We're watching two kids go through growing pains and be open enough about it to sort of let us discover and experience it while they do," Ms. Price said.
But forget "higher-order thinking." Let's turn to basic mathematical knowledge that every sixth-grader should know, but many of my students (more and more each semester) do not. And I know they don't know these things because I have to explain them in class. Students do not know
- what a rate is: I have more than a few students who do not understand why they cannot just add the tax rate to the item price to get the total sale price.
- basic addition and subtraction: I have more than a few students who do not understand that you subtract the cost from the revenue to get the gross profit margin, or do not know that to get the total costs, you add the fixed and variable costs.
- basic multiplication and division: I have more than a few students who do not know that they must mutiply the number of units by the unit cost to get the total cost. I have more than a few students who do not know that because the interest rate is annual, they must divide it by 12 to calculate the monthly amoritization table.
- the relationship between multiplication and division: When we start doing optimization problems in Excel Solver, I have to tell students that because Solver does not like division, they must construct their problem with multiplication instead, and I have many students who do not know or understand how to do this (I also have more than a few students who do not know that you cannot divide by zero.)
- what an arithmetic mean is: I have more than a few students who not only do not understand what a mean is, but seem unable to grasp the concept. It goes without saying that they also do not grasp any statistical concept beyond the arithmetic mean.
Just a note that I heard echoed from several of the summer math program attendees. The Japanese mathematics curriculum is just as strong as Singapore's. Singapore syllabus wins because it's already in English.How can we be sure the data is comparable?
The International Study Center at Boston College works to ensure that data collection procedures across countries are comparable. To this end, the International Study Center institutes the following procedures for quality assurance:
- Coordinated by the TIMSS Sampling Referee, national school and student samples are rigorously reviewed for bias and international comparability.
- Utilizing two independent translations within each country, the TIMSS materials are translated into the national languages of the participating countries. Once these translations are reconciled, the International Study Center verifies these results through the use of a professional translation agency.
- National Research Coordinators (NRCs) and their staff are thoroughly trained in data collection and scoring procedures at international conferences designed specifically for this purpose. The TIMSS International Study Center then continues to monitor the work of the NRCs and their staff for scoring reliability.
- Site visits by quality control staff are conducted during the testing period to further ensure the international data collection procedures are being followed at the national level.
- Finally, an extensive review of data is conducted for internal and cross-country consistency.
Questions & Answers
A brief overview of the Singapore educational system:
The system sounds more complicated than it probably is. Visit this page at the Ministry of Education for a nice graphic that shows student options at every level. We noticed several important differences between the US and Singaporean education systems. Perhaps the single most important difference is that the government and people of Singapore view education as an investment in their future. The country’s only natural resource is their citizens and they spend the money to create great citizens. In America, education is viewed as an expense.
Primary
There is no public kindergarten in Singapore. It may be provided as day care, through churches or the political parties. Because of this, students enter P1 with a wide variation of prior knowledge. Remediation begins in P1. Primary students begin their school days either at 7:30 or 8 am and are released around 1:00pm. They buy or return home for lunch, then come back to school for Co-Curricular Activities (CCA). These may include band, sports, tuition (tutoring), dance robotics, video or anything we might consider an “after school activity” See http://www.moe.gov.sg/ccab/ for more information. My conference partner and I got the impression that a certain number of hours in CCAs were required weekly, but it’s possible that this is a school requirement, not a national standard. Remediation is strongly encouraged for certain students and we got the sense that a teacher’s recommendation of tuition (tutoring or remediation) is always heeded.
Because all students are ELL, the emphasis in the first 3 years of primary school is on English, maths and Mother Tongue (Tamil, Mandarin or Malay). In maths, students are ability grouped (called “subject banding”) into 3 groups. Principals refer to it as HAMALA – High Ability, Middle Ability, and Low Ability. Science and social sciences are integrated, but not considered “core” subjects. Science becomes a core subject beginning in P4 (4th grade), however, we found many examples of strong integration in the classrooms we visited (two P1 classes, one P3, two P4). Students sit for the Primary School Leaving Exam (PSLE) at the end of 6th grade. This determines their placement in Secondary School. Student capacity is capped at 40 students in a regular classroom from P3 and up, 30 students for P1 & P2. A music teacher told me she had 80 in her classes.
Info on the change from streaming to subject banding from the MOE website:
SUBJECT-BASED BANDING IN PRIMARY SCHOOL
Key changes
| > | Starting from the 2008 Primary 5 cohort, primary schools will introduce Subject-based Banding to replace the current EM3 stream. Currently EM3 stream students offer the Foundation level for all subjects. With Subject-based Banding, students will be able to offer a mix of Standard or Foundation subjects depending on their aptitude in each subject. For instance, if a student is weak in English and Mathematics, he can choose to take English and Mathematics at the Foundation level while taking Mother Tongue Language and Science at the Standard level. |
Students in the top 1% of ability, based on testing are offered the chance to study at a special school for the gifted.
Below is a diagram of Special Education system for Primary students (Click it to get a better image):

Secondary
Compulsory education is 6 years, so it is possible that some students do not go on with their education beyond P6. Students must submit to several interviews with parents and the principal before they are allowed to end their schooling at this point. Secondary students are placed in a track based on their PSLE. There is the Express Course, Normal Course (Academic) and the Normal Course (Technical) and from there it gets confusing. Try the link under “brief overview” above to the MOE graphic.
During our trip, we visited two secondary schools. Between the two, we observed two Sec. 1 maths classes (grade 7) and a Sec.4 (grade 10) maths class. What we found is that some things are similar the world over. We saw bored students, disruptive students and teachers giving it their all. We also saw highly engaged students, who had high expectations of themselves and their school. Although Singapore no longer ranks schools by their achievement, both schools we visited were still considered mid-tier schools.
The principal at Kuo Chuan Presbyterian Secondary School told us that he still canes students for disruptive behavior in the classroom. It is still allowed in Singapore, but only the Principal may do so and he would never do it publicly, just in front of the class the student had disrupted. We didn’t hear about anyone else still caning, but were surprised to hear about it from the principal at the last school we visited. (Put that down as a topic we wished we had thought to ask about sooner.)
Students take the “O” level exams towards the end of Sec. 4. Normal (academic) students have a 5th year before they take the test. Their score determines if they go on to Junior College (Grades 11 & 12) or a technical school. Many Secondary schools are now affiliated with Junior Colleges. Students in the Express Course can bypass the tests and go straight on to the JC. Maths students that we saw were additionally sorted by “E” maths and “A” maths. The “A” maths consists of an additional course on top of the “E” maths course and is recommended for students going on to any type of engineering or technically advanced coursework. Again, refer to the picture on the MOE website if your head is now spinning.
A bit about the teaching profession:
Teachers in Singapore are valued right below doctors & lawyers, although not paid nearly as well. A teacher just starting out begins at around $24,000 a year after mandatory savings of 7% is taken out. To become a teacher, you must first get a job from the Ministry of Education, and then go to school to get your degree or diploma. After that you may teach full-time, although you are working part time in a classroom while in school. Teachers who have difficulty are immediately given remediation as a poor teacher reflects a poor principal and no principal wants their teacher to be a failure. Teachers only teach three core subjects in the lower primary and four in P4-6. That allows them time to grade every piece of paper that a student turns in, and thoroughly at that. Even with 40 kids in a classroom, I can tell that they have a better grasp on each student as an individual than most teachers in the US.
[I]n regular classrooms we learned that students need to be able to write answers to between 70 and 90 simple addition problems per minute in order to be able to successfully and smoothly master arithmetic story problems. However, some students seemed to level off at around 20 or 30 problems per minute, and no amount of reward or encouragement seemed to help. Some of our colleagues (Starlin, 1971; Haughton, 1972) decided to check how many digits those students could read and write per minute—critical components of writing answers to problems. As you might guess, they were very slow, which held down their composite performance. With practice of the components on their own to the point of rapid accurate performance (for example, reading and writing digits at 100 per minute or more), students were able to progress smoothly toward competence on solving the written math problems.
"I was a Wilton High School student who dozed off while Mr. Laptick taught us dimensional analysis in physical science. I never quite got the hang of it. It irritated me... all of those fractions. I never really liked fractions. Although my grades had been pretty high, I got a D in physical science and subsequently dropped out of chemistry in the first quarter of my junior year. It was not long before I started on drugs, and then crime to support my drug habit. I have recently learned dimensional analysis and realize how simply it could have solved all of my problems. Alas, it is too late. I won't get out of prison until 2008 and even then, my self image is permanently damaged. I attribute all of my problems to my unwillingness to learn dimensional analysis." Jane
"I thought I knew everything and that sports was the only thing that mattered in high school. When Mr. Hoogenboom taught our class dimensional analysis, I didn't care about it at all. I was making plans for the weekend with my girlfriend who loved me because I was a running back and not because of physical science. While other kids were home solving dimensional analysis problems, I was practicing making end sweeps. Then one day I was hit hard. Splat. My knee was gone. I was despondent. My girl friend deserted me. My parents, who used to brag about my football stats, started getting on my case about grades. I decided to throw myself into my school work. But I couldn't understand anything. I would get wrong answers all of the time. I now realize that my failure in school came from never having learned dimensional analysis. Alas, I thought everyone else was smarter. After the constant humiliation of failing I finally gave up. I am worthless. I have no friends, no skills, no interests. I have now learned dimensional analysis, but it is too late." Bill
I was at home, sick with the flu when Mr. Mycyk taught my class about Dimensional Analysis. Despite opportunities given to me to make up the assignments that I had missed, I chose to not do them. I thought that my mathematical abilities were already sufficient. How wrong I was! It’s been five years since I took that class--Now I spend my afternoons panhandling at traffic lights, hoping for passersby to give me spare change. If I ‘m lucky enough to scam a buck after a day’s work, I’m still not sure if my hourly rate makes cents. --Mario
source:
Dimensional Analysis
I managed to pass both intro chemistry and intro physics in college without learning anything at all about either subject just by being able to manipulate dimensions to arrive at an answer for exam questions. In one semester of Chem I even made a B and had no clue about the actual subject matter.
As a former chemistry teacher I would say you cannot overemphasize an understanding of dimensional analysis.
For kids who don't see the point, ask them "backwards" questions such as how many feet are in an inch?
Also, have them do long chains such as determining how many centimeters in a mile. It's good to have figured these out in advance yourself so your student is instantly rewarded if they get the right answer.
To solve word problems about percent, it is necessary to be able to visualize the problem. We will begin to work on achieving this visualization by drawing diagrams of percent problems after we work the problems. Learning to draw these diagrams is very important.
Twenty percent of what number is 15? Work the problem and then draw a diagram of the problem.
We will use ... 20 for percent, WN for what number, and 15 for is.
20/100 · WN = 15
The "before" diagram is 75, which represents 100 percent. The "after" diagram shows that 15 is 20 percent. Thus the other part must be 60, which is 80 percent.
When a problem discusses a quantity that increases, the final quantity is greater than the initial quantity. If we let the initial quantity represent 100 percent, the final percent will be greater than 100. This means that the "after" diagram representing the final quantity will be larger than the "before" diagram. The "after" diagrams in this book will not be drawn to scale. [emphasis in the original]
[snip]
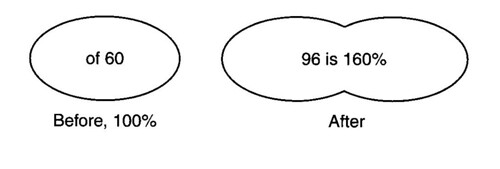
What number is 160 percent of 60? Work the problem and then draw a diagram of the problem.
WN = 160/100 · 60
A method for teaching writing called the "process approach" is on the increase in many school districts. Supporters of the method are admirably enthusiastic. They have publicized it widely through articles in professional journals and worked diligently to stamp out the use of other methods such as sentence combining which they call "unnatural writing" or "mechanistic." [Rousseau alert]
However, there are signs that the process approach may look better in professional articles than in practice. Recent studies show it is not particularly effective in typical school settings....
The growing use of the process approach is reflected by this statement in The Writing Report Card, the report from the National Assessment of Educational Progress on our students' writing skills:
The emphasis in writing instruction moved from the final product to the process--planning, drafting, revising, and editing. As a result, school districts across the country have begun to institute process-oriented approaches to writing instruction.
But The Writing Report Card is not able to give the process approach a high grade:
Some students did report extensive exposure to process-oriented writing activities, yet the achievement of these students was not consistently higher or lower than the achievement of those who did not receive such instruction. At all three grade levels assessed, students who said their teacheres regularly encouraged process-related activities wrote about as well as students who said their teachers did not.
Stunt people were around long before films.Even Shakespeare probably used them in fight scenes.
[I]n regular classrooms we learned that students need to be able to write answers to between 70 and 90 simple addition problems per minute in order to be able to successfully and smoothly master arithmetic story problems.
I love this -
I've been digging into the Writing Skills book from EPS, also. I have book 2.
It works well with The Paragraph Book. Book 2 is a bit more sophisticated than The Paragraph Book, so it feels more like a book pointed towards remedial upper-middle school, or high school.
It delves into formula, but is not so rigid about following a specific one like The Paragraph book.
The Writing Skills teacher's guide is not so much a book with the answers, but a good overall how-to for teachers and parents. I still like answers (even if there's more than one) when I get a teacher's guide, but this guide is really informative.
Writing Skills is very specific with its target concepts, (like The Paragraph Book,) but covers more ground in a more advanced way.
The Paragraph book looks deceptively simple, but it has revealed some interesting things about my son. For instance, book one is all about writing a simple paragraph about how to do something. They have to write several of these kinds of paragraphs with the formula: FNTF (which means First, Next, Then, Finally...)
My son wrote one on how to put toothpaste on a toothbrush. He wrote as sparingly as he could since he thought it was a stupid exercise. I kept telling him he needed more detail, but he argued that he didn't.
Finally, I had him read to me his paragraph while I tried to follow his directions exactly as though I was an alien. After bursting out laughing at my attempts to follow his directions, he finally got what I was saying.
He seems to have no sense of audience.
The goal of timed tests is computational fluency: by this we mean quick and accurate knowledge of math facts. As has been said before to parents in earlier grade levels (and is worthy of repeating), automatic recall of basic math facts is desired because it frees up students’ minds for complex problem solving. To this end, fourth grade students will prepare for weekly timed tests. Below are the details.
What: Each timed tests consists of 50 problems to be completed in four minutes or less, although many students set personal goals of two minutes. Timed tests begin with subtraction facts (0-20) and, in the winter, move to multiplication facts (0-9).
When: Timed tests are given every Wednesday for the entire year. Students keep corrected timed tests in their math binders along with a chart of their progress.
How: We review study tips with students and provide work sheets for practice. Enclosed are strategies for subtraction and multiplication to help your child polish his or her math facts at home. Students can make flash cards of difficult math facts. Additionally, the Lower School’s math library has a variety of math aids available for home practice; materials may be borrowed for two weeks at a time.
please don't tell me that
you're taking "celeration" seriously.
to my eyes, it makes the already
formidable disincentives to teach
look almost pleasant.
if these guys actually
get any influence, i'll be
back on the loading dock ...
"Since 1990 the Standard Celeration Society has comprised a collegial organization for all persons who use Standard Celeration Charts to monitor and change human behavior frequencies."
I'm all in favor of mastery and speed in the basics of math, but I'm not too keen on schools trying to monitor units of behavior frequency change. I would rather have them monitor units of correctness (grading) on weekly quizzes and tests.
Quite fast; I normally see the answer to simple questions without consideration.
Possibly related: In the summer between 4th and 5th grade, the summer school I attended did mad-minute multiplication. We were doing 100 single-digit problems in one minute with 95%+ accuracy.
More generally, I've learned other things by extended rote practice and I still know most of those things with no real thought. (German irregular verbs, typing, judo throws.)
Yes, the practice is tedious for both student and teacher. But the student only has to do it once and the teacher is being paid very well. (Note: the work of a teacher is easier and the pay is better than the work and pay on a loading dock -- I've worked on a loading dock.)