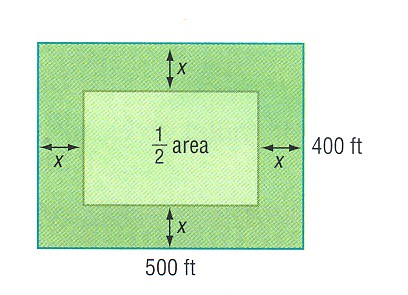
Kirk and Montega have accepted a job mowing the soccer playing fields. They must mow an area 500 feet long and 400 feet wide. They agree that each will mow half the area. They decide that Kirk will mow around the edge in a path of equal width until half the area is left.
43. What is the area each person will mow?
44. Write a quadratic equation that could be used to find the width x that Kirk should mow.
45. What width should Kirk mow?
46. The mower can mow a path 5 feet wide. To the nearest whole number, how many times should Kirk go around the field?
Glencoe Algebra, p. 537
ISBN: 0-07-873316-2
I'm completely befuddled.
The equation I've come up with works when I plug in the book's solution (in Comments section), but I can't use it to arrive at the solution for x to begin with.
Too bad I don't have the answer key.
update: district has now said it will provide the answer key "ASAP. "
We will see.
can you FOIL the answer key?





13 comments:
answers to odd numbers:
43. 100,000 feet
45. about 65 feet
I tried to work the problem, repeatedly, this way:
500x + 500x + (400-2x)x + (400-2x)x = 100,000
When I plug in 65 ft, the answer checks.
I can't for the life of me work the equation and arrive at an answer of 65 ft.
I've just worked this problem for the 10th or 11th time, and now I do get 65 -- but I'm completely balled up on the minus signs.
I end up having to find the square root of -25,625, which I think is: +/- 160i
At that point I'm just guessing whether I want the positive or negative value of 160.
The soccer field is 500 ft x 400 ft = 200,000 ft^2 in area. Each will mow half, or 100,000 ft^2.
The inner rectangle has sides (500 - 2x) ft and (400 - 2x) ft. The inner rectangle is therefore (500 - 2x)(400 - 2x) = 200,000 - 1800x + 4x^2 ft^2 in area. Montega is mowing the inner rectangle, which is half of the total, or 100,000 ft^2. (From here on out, I am dropping the "ft^2" for simplicity, but remember that the area is in ft^2 and the length and width are in ft.) Therefore 200,000 - 1800x + 4x^2 = 100,000. Subtract 100,000 from both sides: 100,000 - 1800x + 4x^2 = 0. Rearrange: 4x^2 - 1800x + 100,000 = 0. Divide both sides by 4: x^2 - 450x + 25,000 = 0.
Solve for x using complete-the-square or the quadratic formula:
x^2 - 450x + 25000 = 0
x^2 - 450x = -25000
x^2 - 450x + 50625 = 50625 - 25000 = 25625
(x-225)^2 = (approx +/-160)^2
x - 225 = approx +/- 160
x = approx 65 ft or approx 385 ft.
Which of these makes sense? Does x = 385 ft make sense? No, because the inner rectangle has sides of (500 - 2x) ft and (400 - 2x) ft, and x = 385 ft would make these negative. So the answer must be x = 65 ft (approx.).
Plug in the answer to check:
Inner rectangle has area (500 - 2x)(400 - 2x) = 370(270), which is 99900, which is close to 100,000.
(This thing won't let me post -- GoogleMaster)
Catherine -- before you write out the equation, look at the geometry. You can either figure out the area of the outer region or the inner region (and, of course,they will be the same). The problem is set up to entice you to do it the hard way, which is the way you set it up, by looking at the path that Kirk mows, and adding its area up as four skinny rectangles.
It is easier to calculate the inner area, which is (500 - 2x)(400 - 2x). Then the quadratic equation becomes, as Anon wrote,
(500 - 2x)(400 - 2x) = 100,000
To solve that, since inspection seems not to work, we have to multiply it out. A good strategy is always to take a breath and look at what you've got before taking something tidy, like this equation in factored form, and multiplying it out. (The word entropy comes to mind.) I don't like leading coefficients. I could factor a 2 out of each set of parentheses, yielding a 4 on the left. The right is conveniently divisible by 4, so I would really work with
(250 - x)(200 - x) = 25,000
Now multiply out, solve, and like Anon did, eliminate the root that comes from (+) in the quadratic formula as physically impossible. Thus you get approximately x = 65 feet. How many times around? The mower path cuts 5 ft, so 65/5 = 13 times should do it.
(I believe that if you manipulate your equation you will get the same thing that the previous Anonymous poster posted.)
The problem is set up to entice you to do it the hard way, which is the way you set it up, by looking at the path that Kirk mows, and adding its area up as four skinny rectangles.
omg
That's exactly what happened.
I solved it the hard way.
Of course I knew the two areas were equal, but I "felt" that I could use variables to define the outside area, but not the inside area.
THANK YOU
eliminate the root that comes from (+) in the quadratic formula as physically impossible
This is the part of these quadratic word problems (which I have never in my life seen or done) that confuses me.
It doesn't make sense to me to eliminate one root as physically impossible ---- it's not that I somehow think that a negative value can be a measurement; I know it can't be.
But it's still surprising to me to be eliminating a root as impossible. Can't explain it.
This is an example of the "wild goose chase" approach to solving problems when you are a rank beginner.
doing things the hard way...
I ended up with one of my factors being the square root of -1.
I'm so grateful to you guys -- you and Barry, who worked the entire "review" sheet I was struggling with this week.
C. is now whizzing through quadratics problems.
Now that all the heavy lifting is done here, I can make two points without feeling guilty:
"district has now said it will provide the answer key "ASAP."
1) "ASAP" = 7 months into the school year
2) Their assurance is probably an elaborate setup for an April Fool's joke. Next week you'll likely get an e-mail containing, "j/k LOL!!!" and "April Fool's!"
"eliminating a root"
I'm assuming you understand why a quadratic equation has two roots. Here's a simple example. x^2 = 4
What is x? It can be either +2 or -2.
Both of them are correct or possible.
Now let's say I add a separate condition (that I've just made up) which is that the answer I want is negative. Then you know the answer is -2 and that the +2 answer is "impossible", i.e. doesn't meet my additional condition.
That's all that's happening in the word problem. There is an additional condition because it is a physical problem: the side of the rectangle has to be a positive number.
Saying that the negative solution is "impossible" is just a brief way of saying that it doesn't meet the additional physical condition of the problem.
Why don't they just divide it in two 200 X 250 ft rectangles like most normal people would (unless they're just finding creative ways to procrastinate doing the actual labor)?
Dividing each dimension in half actually results in quarter lots and not half lots. Using rectangles, you'd have to make the half-lots either 200 x 500 or 400 x 250.
Actually, it is sometimes interesting to ponder the “eliminated solution.” In the case of this problem, we could overlay a coordinate grid on the diagram. Place the origin at the lower left corner of the inner rectangle. From this point, we have computed that the horizontal side of this rectangle goes forward 500 - 2x ft, and the vertical side goes up 400 - 2x ft. This means that when we use our favored solution of x = 65 ft, our horizontal side is length 370 ft, and our vertical side is length 270 ft.
So, what happens when we use the other solution, x = 385 ft? This is going to be a little confusing, because I am going to refer to x and y coordinates. Try not to confuse the x coordinate with the value of the variable x that was computed by Mark. If we start at our origin and move 500 - 2(385) ft in the x direction, we end up going backwards to coordinate x = -270. If we move 400 - 2x in the y direction, we go down to y = -370. So, if we consider the rectangle with opposite corners at the origin (0,0) and the point we reached (-270, -370), we have once again outlined a rectangle that is 370 ft by 270 ft. It’s just that it is oriented with the longer side vertical instead of horizontal. It is also located in Quadrant III instead of Quadrant I. So, it is still a plausible solution to the problem in some sense.
I have found geometric significance to other “eliminated” solutions in quadratics. I don’t have the graphics ability in this comment space, but if you consider problems involving secant segments meeting at a point outside a circle, depending on which length is your variable, you can end up with a quadratic. The “keeper” solution is a positive number telling you how far to extend the segment in the positive direction. The “eliminated” solution will tell you how far to go in the negative direction to take the chord across the circle and emerge the same distance out the other side of the circle.
When you eliminate a solution, it can still be interesting to consider what it represents.
Dan K.
Post a Comment