percent problem from Math Notations

A percent problem at Math Notations:

There are 20% more girls than boys in the senior class. What % of the seniors are girls?

The Comment thread is fantastic, as is the thread on the follow-up post.

And here is Denise, of Let's Play Math, on the subject of percent:

Percents are one of the math monsters, the toughest topics of elementary and junior high school arithmetic.

Now she tells me.

As it happens, I agree. Percent problems are he**. That is my final word on the subject. H-e-double hockey sticks.

I am spending my entire summer trying to teach percent to you-know-who, when I had planned to spend my entire summer practicing up on factoring polynomials and such.

Turns out factoring polynomials is child's play compared to decimals, fractions, and percent.

Back to Denise:

The most important step in solving any percent problem is to figure out what quantity is being treated as the basis, the whole thing that is 100%. The whole is whatever quantity to which the other things in the problem are being compared.

Denise's post, which she calls the search for 100%, puts me in mind of Ron Aharoni's book, Arithmetic for Parents (scroll down). Carolyn and I both loved Aharoni's article for American Educator, What I Learned in Elementary School.

Here's his passage on the fifth operation of arithmetic:

In addition to the four classical operations, there is a fifth one that is even more fundamental and important. That is, forming a unit, taking a part of the world and declaring it to be the “whole.”

I love that!

So, on to our problem. The folks at Math Notations discuss the ambiguities of the English language in percent problems. I found the problem's wording ambiguous myself, and used a bar model to clear it up:




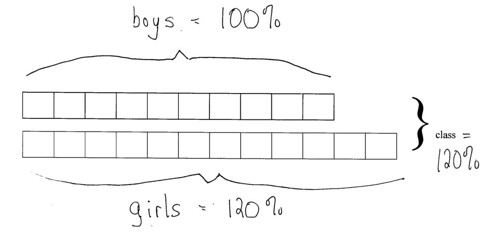
large image here

In the bar model the number of girls is definitely 20% greater than the boys. Plain as day. However confused you may have been by the words, there aren't a lot of different ways to draw the girl bar, assuming you've drawn the boy bar correctly (which you won't have done if you're a middle school student, but never mind).

After you've drawn a 10-square bar model to represent the boys and a 12-square bar model to represent the girls, you see that to get the total class size you're going to have to add 100% to 120%.^* There is just no way around it.

Without a bar model (and even with a bar model) this is brutally confusing, because in everyday language "whole" and "all" mean "100%."

It's difficult to break set, as my cognitive psychology professors used to say.

Making boys the "100%" requires big-time set-breaking, because when you're given a problem involving boys and girls in a class at school, you think of the boys as the boy-part of the class and the girls as the girl-part, with the class being everyone, i.e. the whole, i.e. 100%.

The idea of adding 100% to 120% to get a class of 220% is just frankly nuts in terms of everyday language and experience. A class can't be 220%. We know this.

..........................

I wonder if this problem would be more solveable if you wrote it in nonsense words?

There are 20% more meps than jeps in the pile. What % of the pile are meps?

None of those words, including "pile," screams out at you: I am always and forever 100%; trifle with me at your peril.

.................................

I walked Christopher through this problem.

Just because I could.

.................................

update from Susan J:

To me the most natural way of doing the original problem is two equations in two unknowns:
Either
g = 1.2 b
g+b = 1
and then convert the answer to per cent or

100 g = 120 b
g+b = 100

The one encouraging aspect of the two posts at Math Notations was that apparently kids who know algebra pretty well can solve this problem. I assume they use Susan's two equations, but I don't know.

Actually, that was very encouraging.

On a related subject, I'm moving into the Saxon/Dolciani "percent charts," in an effort to bring home the idea that if you have 20% more girls than boys you will have 1.2b -- only I'm starting with a whole of 100% (I wonder if that's a bad idea...)

The charts look like this:

original price 100% $50
discount 10% $5
new price 90% $45


A word problem would be something like this:

Catherine bought a new blouse for $45. It had been reduced by 10%. What was the original price?

original price 100% p
discount 10% $45
new price

The charts help you see that if you're taking 10% off the price, then you're paying 90% of the price (something I didn't realize until two years ago, when I did a percent problem in Saxon).

I'm having a terrible time getting C. to see that we're dealing with proportions here, and that percent problems can always be solved as proportions -- and that the chart is a cool way to show you all the various proportions you can employ to deal with simple problems like these.

Probably time to back up to something simpler.

Tomorrow I'm going to have him do a page of equivalent fractions using percent fractions and non-percent fractions.

e.g.:

75% off $60 means:

25/100 = x/60

I'll try to combine these with the charts and see how that goes. Must re-read Dolciani & Saxon, too.

..................................

Fantastic posts and threads:

The search for 100%
wrong answer: girls are 60% of the class
there are 20% more girls than boys
percent word problems revisited

and, at ktm-1 (you may have to hit refresh a couple of times):
Aharoni article, part 1
Aharonic article, part 2
Ron Aharoni on the 5th operation of arithmetic
Ron Aharoni on teaching fractions

order Arithmetic for Parents
Ron Aharoni's home page


^* or 10 to 12, as the case may be