source:
Primary Mathematics Intensive Practice 3A, U.S. Edition
p. 8
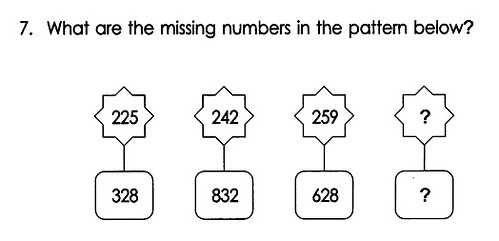
I absolutely cannot see what comes after 628.
Having looked the answer up in the back of the book, I absolutely cannot see why 862 should come after 628.
I hate number patterns.
They do what they do.
Thinking about schools and peers and parent-child attachments....I came across one of my favorite posts .


44 comments:
Before I read your answer, the only relationship I could see in the firt two lower numbers was that the ones and hundreds were reversed. My guess was to reverse the ones and hundreds in 628 resulting in 862. Now I see that this is what the answer key says as well. I'm not really sure how I thought to do that, it was just the only thing I could think of that was happening with the first two numbers. The funny thing is that I assumed I was completely batty and that there must be some mathematical explanation. Is there?
Are they adding 17 in the top layer and rearranging the digits in the bottom layer?
In other words, are the two connected layers actually not connected at all?
I keep trying to figure out why there are lines in between the top and the bottom boxes.
It really doesn't make any sense to me either.
I had A look at it and covered up the answer part. Since this is from 3A she should be able to answer it, right? She said "They're adding 17 to each of the top numbers and the bottom numbers are switching place value." She is very strong at pattern recognition and this was her best guess.
I think the lines between each top number and each bottom number really throw you off. It seems that they're supposed to be related somehow, but I cannot see how they are.
Of course, it leaves me with this sinking feeling that there's something I'm just not getting.
Ok, let's assume that rotating the ones into the hundreds column is the correct answer. How do you go from 832 to 628? That's what was throwing me off - even if the top number has no relationship to the bottom number (which is absolutely ridiculous, given the layout of the problem), the top line at least involves pattern from the first to last. The bottom series consists of two unrelated pairs.
Leaving aside the complete lack of mathematical content in this particular pattern, there's no clear logic to dictate why that pattern would be correct.
Oh well. At least the numbers weren't in alphabetical order, or something like that.
I think that the next number on the bottom should be 1132, followed by 928. (This answer isn't any more valid than theirs is, but I don't see how it's less valid.)
BTW, this is a reason to doubt any such pattern recognition exercise, particularly when the pattern is so short. There's nearly always another pattern that fits just as well as the "correct" answer, but that the test writer didn't think of.
I also think that absent other context on the page, the series on top and bottom are unrelated and the lines are misleading. But if you wanted to force things, you could certainly create a rotated hyperbola that used the line defined by the top values as the axis of reflection and the points on the bottom line as y-values for regular increments of the x axis. It wouldn't be elegant or particularly intuitive, but it certainly wouldn't be "wrong".
This points to something that I find interesting about mathematicians: When presented with a problem of this sort, a mathematician will nearly always look for the most elegant answer (for some value of "elegant"). And there will be a fairly strong agreement among different mathematicians about what constitutes elegance, even though most of the mathematicians wouldn't be able to rigorously define what they are seeing.
With appropriate use of constants and coefficients, I could, for instance, fit some sinusoidal monstrosity to the top values and get something deeply unintuitive for the final answer. But that answer would not be elegant, so it would violate an unstated premise of this sort of problem. That's fine when you've been indoctrinated into the mysteries, not so much for third graders.
The advantage of being a mathematician is that you can cover up your lack of insight with big words:
The top sequence is linear (add 17 each time), so if there is a reasonable way to match up the top series with the bottom, there is also a reasonable match of the bottom to the integers 1, 2, 3.
Looking at successive differences between terms (832-328 and 628-832) yields the information that there are no common differences. With 3 terms, the sequence can always be matched to a quadratic sequences by assuming common differences of differences, which would yield the fourth lower term of -284. There is insufficient information to discriminate between my fourth term and theirs (no good reason to choose 862 over -284), so I declare it to be a poorly posed problem.
Since this is from 3A she should be able to answer it, right? She said "They're adding 17 to each of the top numbers and the bottom numbers are switching place value."
Good God.
Is that what they're doing?
That's ridiculous.
Wait.
I'm totally confused.
Where did the 6 come from?
Or is the 628 the start of a new pattern?
Who knows? This is very unlike anything I've ever seen in Singapore Math (we've not done 3A/B). But yes, it appears the bottom two numbers are sets. The third number is not related to the first two.
There was no additional set of numbers? Was there a similar example in the textbook? Really weird.
YES, the only way that "guess" works is if the 628 begins a new pattern.
Questions like these are on Mensa tests.
The whole idea is to challenge the folks who can't accept obviousness (or those who tend to cling to algorithms).
It reminds me of the old business-type test here.
Does it belong in a primary math book? Nope. But still.
There IS a pattern, and it is given; i.e., it is obvious (too obvious).
Can two different people extend the pattern differently? Yes. But, you see, that idea has nothing to do with the question.
Overthinking is the problem here. And that is--at the very least--interesting.
Does it belong in a primary math book? Nope.
It's not clear to me that Intensive Practice is officially part of the Singapore curriculum or if it's a derivative product by a different publisher sold as a supplement to parents.
The top layer increases by 17.
The bottom layer is a combination of "constant increase" and "number rearrangement"
The link between the top and bottom layer is:
When the top number is an ODD number (alternate numbers are odd), the bottom number increases by 300 from the previous number whose top is also an odd number (225->328, 259->628, 293->928, etc)
When the top number is EVEN, the bottom number is a rearrangement of the previous number (328->832, 628->862, 928->892)
Hope this makes sense.
So the next 3 numbers in the series would be:
UPPER: 276, 293, 310
LOWER: 862, 928, 829
Being able to solve a problem like this might mean something. Or not. Not being able to solve a problem like this doesn't mean anything.
Math is all about applying specific techniques to solve problems. Math is all about tools like regression analysis and Fourier transforms. Problems like this are anti-math. They take time away from real learning.
After you get past simple patterns of differences and products, the value of these problems diminishes greatly. They may be fun, but there is no justification that they are part of a balanced math breakfast. Take away the Count Chocula and you still have a balanced breakfast. It's a better breakfast.
I'm still surprised this is in a third grade book. Even more surprised that it's in a Singapore Math book.
Besides computational skills, Singapore primary math places much emphasis on thinking and problem solving skills. You'll often find questions that require more than just computational skills. For example, given the digits 1, 2, 3, 4, 5, 6, 7, and 8, the pupil is required to form two 4-digits numbers (no repetition of digits) such that the difference between the numbers is smallest.
One of the problem solving heuristics recommended in Singapore's primary math syllabus is "look for pettern(s)". Therefore such questions requiring pupils to examine available data for patterns or relationships are found in Singapore math books.
BTW, this is a reason to doubt any such pattern recognition exercise, particularly when the pattern is so short. There's nearly always another pattern that fits just as well as the "correct" answer, but that the test writer didn't think of.
It's worse than that. There is always another pattern that fits just as well as the "correct" answer. Polynominal theory tells us that for any series of numbers, there exists a polynominal that can be fitted to that series. Therefore, you can take a series of numbers of size n, add any other number on to get a series of numbers of size n+1, and be sure of getting a polynomial that fits.
So to take a trivial example, the series [1,2] can be explained by the polynominal y = x. It can also be explained by the polynimal y = 0.44x^5-6.48x^4+26.00x^3-26.42x^2-18.32x+25.77 (I've rounded the constants). However y = x when x =3 produces 3, while my second polynomial produces 18 when x = 3.
In the case of the [328,832,628] series, the next term in the series is 12.97. Or at least, that's what it is if the pattern generating the series is 8x^6-49x^5+58x^4+49x^3+88x^2+89x+87, (with a fair bit of rounding).
Overthinking is the problem here.
As a kid I always absolutely hated this sort of advice, when I got a problem "wrong" because I read too much into it.
No one could ever explain how I was meant to know when I was "overthinking" something.
Personally I think if "overthinking" gets you the wrong answer, the questioner was underthinking.
"Polynominal theory tells us ..."
Exactly. Math is about tools that help us solve problems WITHOUT having to rely on some sort of vague critical thinking process.
If you happen to be at a level where you need to create new techniques for pattern recognition (or anything else), then early grade work on patterns like this won't help you one bit.
If the question was, "Describe one possible pattern relating these numbers and give the next value(s) in the series," then okay, it can stay. But "find THE pattern" is unadulterated horseshit.
1,2,3,?
(a) x(n) = x(n-1) + 1; x(4) = 4 (counting numbers)
(b) x(n) = x(n-1) + x(n-2) for n > 1; x(4) = 5 (Fibonacci)
(c) x(n) = mod(n,3); x(4) = 1
(d) x(n) = x(n-1) * x(n-2) + x(n-2); x(4) = 8
(e) x(n) = prime(n), where "prime" is the list of all prime numbers starting with 1; x(4) = 5
(f) x(n) = atomic number of nth element considering only alkali metals and noble gases (group 1 and 18); x(4) = 10
(g) x(n) = date of November 2007 considering only Thursday, Friday, and Saturday; x(4) = 8
and when all else fails,
(h) x(n) = x(n-3) for n>3; x(4) = 1
What happens when you tell a 3rd-grader that he's "overthinking" the problem? First, he starts to feel dumb because his brain didn't spit out the answer The Authority Figure was looking for, and he compensates by damping part of his thought processes. Second, the other kids in the class start making fun of him because he's smart, and now he likes school a little bit less. Congratulations! You're on your way to destroying another kid's spirit.
As Doug Sundseth and SC (among others) noted, the sequence admits to more than one correct solution.
(a) When there is more than one correct solution, some students will give one solution and some another.
(b) If the teacher's manual only gives one of those answers and the teacher does not realize that there is a second (third, fourth?) solution, some of the students will be told that their answer is wrong.
(c) Therefore, there will be mislearning for all involved: (1) those students who gave the "right" answer will not be shown how the task was ambiguous, (2) those students who gave the "wrong" answer will be both (i) punished for their work and (ii) not shown how the task was ambiguous, and (3) the teacher will likely wander off thinking that some of the students have dyscalculia.
This scenario is, at least in part, the reason Ziggy insists that teaching demonstrations should routinely admit to one and only one solution. If a demonstration does not admit to one and only solution, the teacher must be prepared to accept all reasonable answers.
Sigh....
A comment on my fourth graders report card:
C. has demonstrated proficiency using rounding, mulitiplication and divison algorithms, but becomes frustrated when I challenge him to think "outside the box" about why something works or when it may not work."
The teacher believes "that in the long run that acceptable levels of frustration will be benefical to his learning."
Will letting my child become so frustrated that it ruins his day be benefical to his learning to think "outside the box"?
What happens when you tell a 3rd-grader that he's "overthinking" the problem?
Well personally my response was to think that the teacher was stupid.
Now I'm older I'm a bit more gentle in my judgments. A bit.
"The teacher believes 'that in the long run that acceptable levels of frustration will be benefical to his learning.'"
Frustration is not a teaching methodology.
Frustration is not a typical initial reaction to a problem. (I don't think that's what the teacher is talking about here.) Frustration usually appears after a lot of hard work. Learning defined by frustration is not a goal. Frustration may be understandable at times, but it's more likely an indication of bad teaching.
Frustration is neither necessary or sufficient. In fact, it should be avoided at all costs. I remember trying to learn a new topic in math. One book was very formal, but impenetrable. I found another book that made it easy (almost).
There is nothing wrong with easy learning.
This is one of my mottos.
Many times I have been frustrated and felt that there HAS to be a better explanation somewhere else. There usually is. My frustration told me that there was a problem. Frustration is not an indicator that learning is taking place.
I tell people that I want my son to know the value of hard work. I never tell them that I want him to know the value of frustration. Learning to work hard might involve dealing with frustration, but introducing (or allowing)frustration in the learning process is not beneficial. There will be plenty of frustration without additional help from the school.
Steve,
I think what is so sad is that you have these kids who really want to do well in math and set such high expectations for themselves, then you have someone come along and yank the rug from underneath them.
To challenge my son and his classmates, the teacher is giving them questions in the "problem-solving realm" (emphasis by teacher). Many of them are still trying to make sense out of the algorithms. At least, my son is ahead in that game. But, I hate to think of those kids sitting there feeling stupid or embarrassed because they don't know how to do math problems.
"As Doug Sundseth and SC (among others) noted, the sequence admits to more than one correct solution."
I think we need to look at this in the proper context. The question is for a grade 3 (primary 3?) pupil following the Singapore primary math syllabus. At this stage, the average pupil is expected to know certain things (knowledge, skills, abilities etc) if he had followed the syllabus from the start at primary 1.
This is not the first question on patterns that the pupil encounter.
In the absence of other "clues" the pupil could look at the series 328 832 628 and assume that, as the third number is 300 more than the first number, the fourth number could similarly be 300 more than the second number (1132).
However, if the pupil had previously been exposed to patterns involving rearrangement of digits, then it can be said that the pupil is expected to spot this pattern in the first 2 numbers and apply it to the fourth number, making 862 the preferred answer. (If not, this could be an opportunity for the teacher to point out the "rearrangement" pattern to the pupil.)
Looking for patterns is one of the problem solving heuristics taught in Singapore primary math. If the pupil is given the top number of 395 and the bottom number of 1828 and asked to give the next number in the series , he will find it easier to solve the problem he if had spotted the patterns.
Next top number -> 395 + 17 = 412
Since top number is an even number, its bottom number is a rearrangement of the previous number (assume pattern is a switch between the first and last digit)
Next bottom number -> rearrange 1828 -> 8821
There may be other patterns involving higher order mathematics but, in the context of the Singapore math syllabus and classroom learning environment, the primary 3 pupil is not expected to know them.
There are a couple of issues here. The first is whether Singapore Math properly prepares the student to find patterns. The second is whether this pattern (or any of this sort) belong in a math curriculum.
I'm a really big supporter of Singapore Math, but I'm not a fan of having kids find patterns past basic differences and products. (linear and non linear patterns) But, if you teach them to look for certain patterns (like swapping digits), then do they get the benefit of finding patterns? What, exactly, is that benefit?
Is spotting digit swapping a skill that's needed by grade-schoolers, or by anyone? If you can't spot that pattern, what does it mean? As far as math is concerned, it means nothing.
There are useful patterns to be able to detect, but swapping digits isn't one of them. This must mean that they see a value in the process of finding unknown or new patterns. If kids know that they have to look for swapped digits, then what are they learning by doing this problem? The ability to run through a mental list of arbitraty patterns to find the one that fits? That's a game, not math.
Dick Feynman talked in his books about studying all sorts of trick problems when he was in high school. I don't think he cared at all about trying to figure them out himself. He just wanted to impress his friends. What really helped him later in life was to learn about line integrals.
In responding to John Wills Lloyd's comments that "the sequence admits to more than one correct solution", I was trying to show that there could actually be a preferred solution. That the pupil had been shown patterns involving rearrangement of digits is but an example. It could be rearrangement of colours or shapes or it may not even involve rearrangement of things. My point was that if a primary 3 pupil was expected to be able to spot the "rearrangement" pattern, then the preferred (or more correct?) answer is 862.
If the pupil can't spot the pattern, he has to use another strategy to solve the follow-up question I gave. If he is weak in logical reasoning, it may mean that he will not be able to solve the question within a reasonable time.
Knowing about patterns does not mean having the ability to spot them in the given data. The pupil needs practice to improve his ability to spot patterns. As George Polya stated, "Mathematics, you see, is not a spectator sport".
The focus is on the "teaching of process" (the ability and skill to identify relationships and patterns and to apply them to solve problems) rather than the "teaching of content" (the pattern itself such rearrangement of digits). The ability to identify patterns is also not an end in itself. This process skill adds to the pupil's "box of tools" for analysing and solving problems. It adds to the pupil's web of knowledge and serves as a foundation for subsequent learning.
Whether patterns belong in a math curriculum depends on one's paradigm of math education.
The Singapore primary math syllabus states that "Mathematics is an excellent vehicle for the development and improvement of a person’s intellectual competence in logical reasoning, spatial visualisation, analysis and abstract thought. Students develop numeracy, reasoning, thinking skills, and problem solving skills through the learning and application of mathematics". It also noted that "the development of mathematical problem solving ability is dependent on five inter-related components, namely, Concepts, Skills, Processes, Attitudes and Metacognition". Math, in the context of Singapore primary math, is more than the application of mathematical tools and techniques to solve problems.
Richard Feynman (1918-1988) had a very brilliant mind. He won the Nobel prize in physics and is regarded as probably the most brilliant, influential, and iconoclastic theoretical physicists. He taught himself elementary mathematics before he encountered it at school. By 15, he had mastered differential and integral calculus. He was also known as a prankster, juggler, a proud amateur painter, and a bongo player. I'd like to believe that such a brilliant mind did not consider studying trick problems a waste of time and that adding trick problems to his knowledge web had, in a small and indirect way, contributed to his later works.
What is the aim of teaching mathematics in the primary school?
Here are a few quotes from George Polya (1887-1985), a mathematician and professor at Stanford University and the author of the classic works How to Solve It, Mathematics and Plausible Reasoning, and Mathematical Discovery.
"The good and narrow aim of the primary school is to teach the arithmetical skills -- addition, subtraction, multiplication, division, and perhaps a little more, as well as to teach fractions, percentages, rates, and perhaps even a little more".
"However, we have a higher aim. We wish to develop all the resources of the growing child. And the part that mathematics plays is mostly about thinking".
"And so I think an essential point in the primary school is to introduce the children to the tactics of problem solving. Not to solve this or that kind of problem, not to make just long divisions or some such thing, but to develop a general attitude for the solution of problems."
"This is the general aim of mathematics teaching -- to develop in each student as much as possible the good mental habits of tackling any kind of problem."
I'm astonished that anyone would call this a "pattern". A pattern is something that occurs with regularity . Moving the last digit of a number to the front might be an interesting operation, but if there is only one instance of it, then it cannot be called a pattern.
To teach students to perceive a pattern from a single instance is to teach superstition and ignorance.
"And so I think an essential point in the primary school is to introduce the children to the tactics of problem solving. Not to solve this or that kind of problem, not to make just long divisions or some such thing, but to develop a general attitude for the solution of problems."
I don't buy this one bit. It's way too vague and opens the door to everything that KTM is fighting against. As I have said many times before, schools love to talk in generalities to get parents to go away, and then they decide on all of the deatils.
If the details are to implement Singapore Math, then I'm behind it 100 percent. However, this kind of talk is used to justify all sorts of horrible math curricula.
The justification for teaching patterns of this sort is not vague homilies, it's a detailed explanation of what skills are being developed in the student.
"To teach students to perceive a pattern from a single instance is to teach superstition and ignorance."
For this pattern, I will agree with anonymous.
"... adding trick problems to his knowledge web had, in a small and indirect way, contributed to his later works."
Yes, well, I read it differently. Besides, I prefer a large and direct approach to math education. If schools can begin to get that right, then I might be more open to a few indirect approaches.
"To teach students to perceive a pattern from a single instance is to teach superstition and ignorance."
I agree that it's ridiculous to teach pupils to perceive a pattern from a single instance.
But... again, we need to look at the given question in the proper context. The given question was from the book "Primary Mathematics Intensive Practice 3A, U.S. Edition". Intensive practice implies that the pupil had already been taught "patterns". The practice questions are meant to improve and hone his "pattern" skills.
I spent some time as an anti-aircraft gunner in my national service days. We were trained to manually engage enemy planes should the radar system fail. To do so we must first be able to identify the enemy aircraft. Initially we were given coloured photographs of the various types of fighter planes to identify. As we progress, the photographs showed lesser and lesser details until finally we could, within seconds, identify the type of plane when given a low contrast picture of a small silhouette of it. (The earlier you spot the enemy plane, the more time you have to engage it.)
I think this also applies to perceiving patterns. As the pupil gains experience in perceiving patterns (builds up his knowledge web), he will need less repetition of a pattern to be able to detect it. In this question, the pupil was explicitly told that he should be looking for patterns. Therefore with experience (from sufficient practice), he may detect the possibility of a pattern given a single instance of it. Sometimes he may be wrong but that is part and parcel of the problem solving process. When the pupil realises that he is not getting the right answer (metacognitive skills - the ability to think or reason about one's own thinking.), he reviews what he had learned about the problem so far and decides on another strategy to solve the problem.
concernedCTparent said:'I had A look at it and covered up the answer part. Since this is from 3A she should be able to answer it, right? She said "They're adding 17 to each of the top numbers and the bottom numbers are switching place value." She is very strong at pattern recognition and this was her best guess.'
This shows that A, with her web of knowledge, could perceive the single instance pattern required to get the textbook answer of 862.
She could have also perceived the other patterns (alternating odd and even numbers at top row, increase of 300 between alternate numbers at bottom row, and the link between the top and bottom rows) but did not mention them as she could answer the question without referring to these patterns.
sc: National service ah? You Singaporean also eh? ;-)
"You Singaporean also eh?"
Only Singapor got national service meh? Taiwan and Korea also got what. Aiya, this is international forum. No Singlish. must Speak Good Engish.
(My apologies for this off-topic remark.)
Yes, I'm a Singaporean.
Ah, but that is why I had to confirm. ;-)
And who say Singlish not good English? Legitimate creole what. (C'est pourquoi il faut apprendre la linguistique!) Even if the ang moh here catch no ball, always got CassyT to translate arso.
At this stage, the average pupil is expected to know certain things (knowledge, skills, abilities etc) if he had followed the syllabus from the start at primary 1.
Of course the non-average pupil may have a big sister at home rabbiting on about polynominal theory.
There's no reason to assume that pupils will only be exposed to the things they are taught at school.
When the pupil realises that he is not getting the right answer (metacognitive skills - the ability to think or reason about one's own thinking.), he reviews what he had learned about the problem so far and decides on another strategy to solve the problem.
But in the case of numerical patterns, any answer is right. There's no such thing as a wrong answer, because you can always create a polynominal to fit any numerical series. So therefore how can a student get the wrong answer to a numerical pattern question?
Identifying aeroplanes is a different task as it is not numerical. It is also limited by the possible shapes aeroplanes can take while still being able to fly. Abstract numbers are not so limited.
As the pupil gains experience in perceiving patterns (builds up his knowledge web), he will need less repetition of a pattern to be able to detect it.
You may have learnt this. I learnt the opposite. As I built up my knowledge web, I learnt more and more about the impossibility of predicting a series from a sample of it.
Take the case of a turkey. A turkey may be fed by the farmer for 100 days in a row. Does that mean the turkey will be fed forever? Nope. One day the farmer will kill the turkey instead of feeding it. There is no theoretical reason that merely looking at existing numbers in a series will tell you what the next number is independent of information about the underlying series.
Any test on pattern-recognition should allow for a student who recognises this.
There are always the exceptions at both ends of the bell curve for which the standard curriculum may not be appropriate.
Those at the lower end will take foundation math, attend Learning Support Programme while those at the extreme lowest end will attend special schools for slow learners. Those at the higher end will transferred to the gifted education programme. The rare few with genius potential will probably have to make special arrangements to attend courses at colleges and universities or resort to private home teaching.
Then there are those with varying degrees of Dyslexia, ADHD, Asperger's syndrome, Dyscalculia, etc.
It is impossible for a standard curriculum to cater to the full range of students' abilities, aptitudes and attitudes
"Identifying aeroplanes is a different task as it is not numerical. It is also limited by the possible shapes aeroplanes can take while still being able to fly. Abstract numbers are not so limited."
Well, not as simple as just looking at still pictures. As the fighter plane appears over the hill, it is moving very fast in a continuously changing path. From a stationary point of view (and under varying weather conditions), the silhouette of a moving plane is continuously changing.
"My guess was to reverse the ones and hundreds in 628 resulting in 862. Now I see that this is what the answer key says as well. I'm not really sure how I thought to do that..."
That's the wonder of the human brain. Lets not underestimate the power of the human mind.
A child is able to detect a person's emotion through tone of voice and body language, make up a story given a picture, solve puzzles, imagine, visualise, fantatise etc. without knowing exactly how his brain works. For example, the child can anticipate the trajectory of a bouncing ball without knowing anything about the physics of motion, gravity, friction, etc. I believe that with training and practice, the average primary 3 pupil can perceive the possibility of hidden patterns. After all, the types of pattern that the pupil is expected to recognise are limited.
"in the case of numerical patterns, any answer is right ..... So therefore how can a student get the wrong answer to a numerical pattern question?"
Does this mean that:
1) Given a series of numbers, there can only be one pattern - the no-pattern polynominal pattern
2) Any other perceived patterns are invalid or useless "because you can always create a polynominal to fit" the series of numbers.
3) Assuming that there can be more than one co-existing pattern, we should not teach a student to perceive the second, or third, or fourth pattern and check that he had perceived them correctly.
4) A student can never get the wrong answer if asked to give the next number to the Fibonacci series 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ?
Imagine a primary 2 child walking with her father along a foot path. As they walk past the lamp posts, she calls out the number written on the posts: 2 4 6 8 10 12. She then says to her father, "I bet the next number is 13". The father replies "right". She sees the number "14" at the next lamp post and was disappointed. The father consoles her and tells her that her guess was not wrong as it could be any number. She brightens up and say "I bet the next number is 15". Again, she was disappointed that the actual number was 16. The father assures her that she was correct and explains polynominals to her. She brightens up and say "huh??, I bet the next number is 17".
"As the pupil gains experience in perceiving patterns..."
"You may have learnt this. I learnt the opposite. As I built up my knowledge web, I learnt more and more about the impossibility of predicting a series from a sample of it."
I was referring to the few weeks or months that a primary 3 pupil spent learning (and practicing) patterns. I think you are referring to a much longer period of learning.
You have made a very important observation here. It was only after you have acquired a certain level of knowledge and understanding of numerical series (and other supporting knowledge such as algebra and polynominals) that you were able to appreciate "the impossibility of predicting a series from a sample of it". You must understand a theory first before you can begin to disprove it.
As mentioned before, we need to consider the given question in its proper context.
A primary 3 pupil is just starting to learn the concept of patterns. The subject matter must necessarily be simplified so that the pupil (with his limited knowledge web) can grasp the concept being taught. Education is a progressive building up of knowledge and not a "all or nothing" event (teach them all about numeric patterns or don't teach them anything). We are looking at a work in progress here, not the end product. Whether the primary 3 pupil will ever progress to a stage where he can appreciate "the impossibility of predicting a series from a sample of it" depends on the educational path he takes.
(I'm not familiar with the polynominal theory. However, it seems from your description that it is more suited for getting an approximate rather than an exact fit to a series of numbers.)
"However, it seems from your description that it is more suited for getting an approximate rather than an exact fit to a series of numbers."
Polynomials are a tool that can be used for all sorts of things, including exact interpolation or approximation.
"You must understand a theory first before you can begin to disprove it."
Patterns is not a theory at this level. There are mathematical tools that can be used to identify patterns in data, but this has nothing to do with grade-school math. Learning about pattern recognition is something you do only after you have had a lot of prior math. It takes math to do pattern recognition, not just sitting around and thinking.
My problem with this pattern is that it has gone way past simple linear and non-linear patterns useful for this grade level. There are useful patterns and there are all sorts of silly, trick patterns. All patterns are not equal. Identifying certain useful patterns is a needed skill. The process of identifying unknown and infinitely-variable patterns is not a useful goal. It's not even useful in an indirect fashion. It's a time waster. This is what I fight at KTM - indirect, time-wasting educational ideas.
Overall, this is a minor issue with Singapore Math. However, it is a large driving force in all reform math. The process of looking for patterns becomes more important than the patterns themselves. Guess and check. Discovery learning. The process is more important than real content and skills. Patterns fit right in with this philosophy.
Certain patterns are important, but these patterns can be learned when you cover the material; linear, non-linear, exponential, logrithmic, sinusoidal, and so forth. These are important patterns. All of them can be learned in context.
Some might believe that looking for unknown and arbitrary patterns is a useful skill to develop. However, this skill will be developed better by learning a lot of math, not the other way around.
"It takes math to do pattern recognition, not just sitting around and thinking."
Depends on the definition of pattern recognition. Pupils can recognise patterns involving graphics and shapes such as those found in IQ tests without math. Similarly, looking at numbers beyond its numerical value, they can recognise patterns involving rearrangement of digits. Even with numerical patterns, humans sometimes spot the patterns first through observations (sitting around and thinking?) before using math to validate their observations.
"The process of looking for patterns becomes more important than the patterns themselves. Guess and check. Discovery learning. The process is more important than real content and skills."
Both the process and content skills are important in solving challenging problems. Just knowing the multiplication tables and the algorithm for multiplication and division (content skills) does not mean that the pupil can solve problem sums. He needs to first analyse the problem sum and come up with his plan of action (process skills) to solve the problem. Only then will he apply his content skills to carry out his plan.
"Some might believe that looking for unknown and arbitrary patterns is a useful skill to develop. However, this skill will be developed better by learning a lot of math, not the other way around."
As with many other skills (mental and physical), the earlier the child starts to develop his pattern recognition skill, the better his chances of mastering the skill later on after learning a lot of math.
"My problem with this pattern is that it has gone way past simple linear and non-linear patterns useful for this grade level"
If the goal of primary math education is strictly the study of mathematics, then yes, patterns that does not require the use of math to define may not be relevant. Similarly, other topics that does not involve mathematical computations at this stage such as tessellations, nets of solids and line of symmetry are not relevant.
My view is that primary education should be more than just the teaching of subject content. As a child's brain/mind is developing rapidly in the pre-teen years, primary education should also strive to develop the child's cognitive abilities and skills - logical reasoning, problem solving, spatial perception, etc through math; observing, classifying, etc through science; and linguistic ability, communication skills, etc through English and mother tongue.
"and linguistic ability, communication skills, etc through English and mother tongue."
Wah.... spoken like a true Singaporean.
The term "linguistic" is bandied about too much nowadays however. Strictly speaking, linguistic skills relate to the ability to grasp the (universal) concepts of language -- concepts that transcend prescribed grammar. Otherwise, one could call woodshop "engineering" too.
Children would benefit from realising from young the distinction between morpheme, phoneme and grapheme, and not necessarily knowing the jargon, but the concepts, which will prove especially useful when analysing other languages, grammars, dialects and creoles, and the recognising the different patterns of language in diverse situations of life. In 100 years the lingua franca may be Esperanto instead. I believe there is a project that aims to teach children all the hundreds of phonemes within human capability from a very young age, which is not daunting that young, since the language module is still quite sensitive at that age. Later in life they won't suffer language insensitivity, or worse, intolerance.
"My view is that primary education should be more than just the teaching of subject content."
"more"
The issue isn't "more". It's instead of. Patterns are used in fuzzy math to replace proper content and skills. In the case of Singapore Math, searching for arbitraty patterns might be forgiven, but it's a real issue for other curricula. And if you want "more", I could come up with a lot better "more" than the pattern given in this thread. A vague definition of the benefits of more is not good enough. You have to evaluate the more on a case by case basis.
"Intensive Practice," the book from which this problem was taken, is not an offical Singapore product (the copyright is not held by the Curriculum Planning and Development Division Ministry of Education Singapore) but a "supplement" made by a private company (Novel Learning Centre) and is used by parents at home rather than in classrooms.
It's "Singapore" math only in the sense that it's created by a Singaporean but it's not "Singapore Math" part of the official program.
Saxon math is American. Wal-Mart math workbooks are American. Wal-Mart books have bad teaching in them, therefore Saxon math has bad teaching in it.
And at any rate, you still don't see, "If this pattern were a color..."
'The issue isn't "more". It's instead of. Patterns are used in fuzzy math to replace proper content and skills.'
Yes, proper teaching of subject content and skills is a must.
Post a Comment