kitchen table math, the sequel: help desk

Wednesday, June 13, 2007

help desk




Can this problem be done?

What am I missing?



answer check:

An angle has a measure of 3x - 20. In simplest form, what is the measure of its supplement? Show all work.

180 - (3x - 20)
180 - 3x + 20
200 - 3x

Right?
Posted by at

17 comments:

Forty-two said...

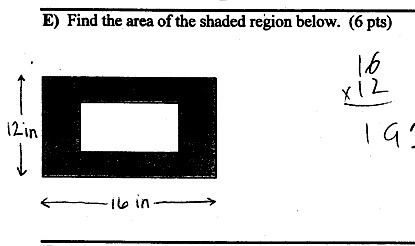
Well, the easiest way to find the area of the shaded region is to subtract the area of the white rectangle from the total area. You can also divide the shaded region into smaller rectangles and compute the area of each and add them up. However, there isn't enough info on the bit you've shown to come up with a numerical answer; is there any further info given on the dimensions in some other part of the problem?

June 13, 2007 at 10:23 AM
Forty-two said...

I would agree with your answer for the angle supplement - was it marked wrong or does the answer key have something different?

June 13, 2007 at 10:29 AM
Catherine Johnson said...

However, there isn't enough info on the bit you've shown to come up with a numerical answer; is there any further info given on the dimensions in some other part of the problem?

That was my question.

This is all the info provided.

It can't be done, right?

June 13, 2007 at 10:42 AM
Catherine Johnson said...

I had a brain-freeze on the second problem - same one C. had.

I thought this was supposed to have a numerical answer; then this morning I realized it wasn't.

Just checking to make sure I did it right.

June 13, 2007 at 10:42 AM
Forty-two said...

Well, technically you CAN do it:

Let x be the height of the white rectangle and let y be width. Then:

Total area = 12in x 16in = 192in^2

White rect area = xy

Shaded area = 192in^2 - xy

Not the most useful answer, but AN answer.

There really was NO further info supplied than the height and width of the outside rectangle? Nothing about the relationship between the inner and outer boundaries, such as the shaded area is a uniform "x" inches deep or anything like that? I'm just having trouble comprehending that. Weird.

June 13, 2007 at 10:55 AM
Anonymous said...

No, it can't be done.

June 13, 2007 at 11:25 AM
Anonymous said...

You could have some fun by measuring the sides, finding the ratios, deducing the unknown values, and then calculating the area. This would be a "hands-on" solution.

June 13, 2007 at 11:35 AM
Nakonia (Niki) Hayes said...

It cannot be done.

You need one side of the white rectangle showing a length. Then, you could set up a proportion to find the unknown side. Or, if the drawing were on a graph, showing the dimensions of the shapes used in the graph, you could figure it out.

This is typical of drawings in geometry problems--the leaving off of a number that is needed to solve the problem.

Niki

June 13, 2007 at 11:44 AM
Catherine Johnson said...

Thank you!

It's funny, because I'm.... not bad at algebra 1.... but I'm still not confident enough to assume that I'm not missing something.

I looked at this and thought: this can't be done.

But then I thought: I'm missing something.

This was it; this was all the information given ON A TEST.

Christopher got this one wrong.

June 13, 2007 at 1:05 PM
Catherine Johnson said...

The new assistant superintendent of curriculum is so good (thus far) I've been contemplating pulling out all the grade disputes we should have had with Ms. K over the years...

But that would be wrong.

June 13, 2007 at 1:06 PM
Catherine Johnson said...

Talking to the new super was almost surreal.

It was like being a person again.

June 13, 2007 at 1:06 PM
Doug Sundseth said...

Even forty-two's answer is over-specific. As written, you can't even determine the size of the figure without considering the cutout. None of the edges are specified as either parallel or perpendicular. Similarly, you cannot specify the size of the internal cutout, because you don't know that it's a rectangle (in addition to not knowing the length of any side).

Certainly, both figures look like rectangles, but this is a math test, not a carpentry test. Precision is required.

June 13, 2007 at 6:20 PM
Catherine Johnson said...

None of the edges are specified as either parallel or perpendicular. Similarly, you cannot specify the size of the internal cutout, because you don't know that it's a rectangle (in addition to not knowing the length of any side).

Certainly, both figures look like rectangles, but this is a math test, not a carpentry test. Precision is required.

I have to get you to take a look at one of the Singapore problems.

I can't tell whether the same issue pertains. (Will have to scan it.)

Do you need to specify that a figure is a circle?

June 13, 2007 at 7:22 PM
Catherine Johnson said...

I think I found another wrong answer on one of Christopher's old tests tonight.

I can certainly see why "Math Dad" was so exercised about the tests & the grading.

June 13, 2007 at 7:23 PM
SteveH said...

You have to look at the questions in context of what was studied in class. The second question says:

"In simplest form.."

This is a clue that tells you the answer is probably an expression. I would also assume that the class has studied a little bit about algebra and knows what "simplify" means.

The first problem looks like a labeling mistake, but after seeing the second problem, perhaps the course required students to define variables as needed. If so, then forty-two's response is correct.

I like Doug's response, but I don't think that would earn you any Brownie Points with the teacher. You could, however, say that you were applying your critical thinking skills.

That reminds me of the old right triangle problem that asks the student to "find" X.

June 13, 2007 at 7:55 PM
Doug Sundseth said...

Oh, if I were in the class, I'd probably reply something like:

"Assuming that the complete figure is intended to be a rectangle, and that the unshaded portion of the figure is also intended to be a rectangle, and assuming that the figure is intended to be drawn on a Euclidean plane, (forty-two's answer). (I wouldn't have included the Euclidean plane part in Jr. High. 8-)

Being a snarky SOB isn't a new thing for me, and that problem deserves snark.

Conventionally, a circle is either explicitly defined as such or shown with an explicit radius or diameter.

June 13, 2007 at 10:06 PM
Anonymous said...

Certainly, both figures look like rectangles, but this is a math test, not a carpentry test. Precision is required.

This may be an unwarranted assumption! :-)

In any event, I was thinking about the snarky solution of copying the diagram to cardboard. Then cutting out the outer rectangle and weighing it. Then removing the inner rectangle and weighing it.

Now I have the ratio of the two areas. I can calculate the outer area ... so I can finish the problem.

Whoo-hooo! Go me!

-Mark Roulo

June 14, 2007 at 8:56 AM

Post a Comment

Subscribe to: Post Comments (Atom)