To solve word problems about percent, it is necessary to be able to visualize the problem. We will begin to work on achieving this visualization by drawing diagrams of percent problems after we work the problems. Learning to draw these diagrams is very important.
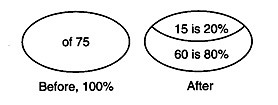
Twenty percent of what number is 15? Work the problem and then draw a diagram of the problem.
We will use ... 20 for percent, WN for what number, and 15 for is.
20/100 · WN = 15
The "before" diagram is 75, which represents 100 percent. The "after" diagram shows that 15 is 20 percent. Thus the other part must be 60, which is 80 percent.
large image here
.............................
The first time C. tried this problem he found it quite difficult. (And, yes, we're talking about a kid who is 1/3 of the way through Math A: algebra 1/geometry.)
Fortunately I stumbled upon the precision teaching folks at that point, and realized I needed to teach the component skills separately. In this case, C. needed practice drawing and labeling the diagram, so I had him do only that for 3 sessions, I think.
Then we did word problems like the one above.
We moved to "story" problems accidentally, "story" problems meaning:
"Jane and Faye have 32 bagatelles left. If they began with 160 bagatelles, what percent of the original number remains?"
(I managed to assign a story problem accidentally because I was flipping through the solution manual looking for solutions with ovals in them, and didn't realize the solution I'd found was a solution to a story problem, not a word problem. fyi)
C. didn't recognize that the story problem could be solved using the same ovals and percent equations he uses to solve percent word problems. Talk about hyperspecificity. I was so wrong to say autistic people and animals are hyperspecific and the rest of us aren't. God is punishing me.*
Today I need to locate the first Saxon lesson on percent story problems and teach that directly.
Nevertheless, in spite of my bumbling, this method is slowly but surely leading C. to some comprehension of what is happening when you take a percent of something in the real world, if you'll pardon the expression.
Speaking of the real world, what is a bagatelle?
I'll post a screenshot of the oval diagrams he uses for problems in which the solution is more than 100% later.
.............................
update: Saxon oval diagrams for problems in which the solution is greater than 100% of the original quantity
When a problem discusses a quantity that increases, the final quantity is greater than the initial quantity. If we let the initial quantity represent 100 percent, the final percent will be greater than 100. This means that the "after" diagram representing the final quantity will be larger than the "before" diagram. The "after" diagrams in this book will not be drawn to scale. [emphasis in the original]
[snip]
What number is 160 percent of 60? Work the problem and then draw a diagram of the problem.
WN = 160/100 · 60
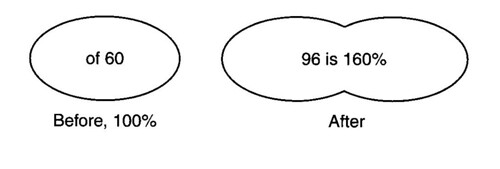
large image here
* I don't say that with disrespect. God should punish me.
hyperspecificity in autism
hyperspecificity in autism and animals
hyperspecificty in the rest of my life
hyperspecificity redux: Robert Slavin on transfer of knowledge
Inflexible Knowledge: The First Step to Expertise
Devlin on Lave
rightwingprof on what college students don't know
percent troubles
what is 10 percent?





8 comments:
"Speaking of the real world, what is a bagatelle?"
I think it is a nice touch that can be appreciated on many levels. It could simply be a way to make the text more literate. It could be a subtle way to poke fun at the "real-world" crowd since it demonstrates that what is important in math is understanding how it works and not the name of some real world object. If you are hungry it can also trigger thoughts of some type of crusty and crunchy French bread. Otherwise, you might just learn another word for trifle.
I thought it was a musical composition (what was I thinking of?), which is what I told C - not having read the story problem closely.
Then today I looked it up on Wikipedia and thought, "Huh?"
I like what's called the part-whole-percent setup.
Basically, most percent problems in elementary/middle school math have two of these three pieces of information (part, whole, percent) and one missing.
The setup is part/whole = percent/100.
Twenty percent of what number is 15?
First, write the percent: 20/100.
Then identify the part and the whole (sometimes tricky, which is why you get the percent out of the way first). Here the part is 15 and the whole is missing.
So you get 15/? = 20/100.
Jane and Faye have 32 bagatelles left. If they began with 160 bagatelles, what percent of the original number remains?
The percent is missing, the part is 32, and the whole is 160.
32/160 = ?/100
The rest is just* using cross products to solve proportions.
*not to insinuate that solving proportions is a walk in the park for kids
When doing percent word problems students should be able to translate into an equation (after converting % to a decimal or fraction). The method could be called percents in translation. Thus "is" is =, "of" is multiply, what is the unknown. It works like magic. Saxon 87 does a good job showing this.
I like what's called the part-whole-percent setup.
Absolutely.
I was talking to Barry about this. I didn't learn part-whole-percent until 2 years ago.
Same thing with ratios.
I was basically stunned to "find out" that if you have 3 girls for every 4 boys you have a grand total of 7 kids.
I read "bagatelle" and immediately mentally hear Les Mis. :-)
http://www.allmusicals.com/lyrics/lesmiserables/lovelyladies.htm
-m
Does the concept of profit speed up the process a lot?
I mean, after playing lemonade stand for a while, kids come to realise that their revenue isn't actually the real amount of money they make, but rather, there is a certain approximate rate between profit and revenue.
But I assume, "You are selling lemonade for 25 cents a cup; the cost to make each cup is 10 cents, how much cups do you need to sell to make a profit of X dollars" is pretty standard?
What the PSLE liked to do is set different rates for buying individually and buying in bulk. Or sometimes you had to buy a fixed amount first, then after buying X amount of goods at P dollars each, you could buy Y amount of goods at Q dollars each. Then exam questions would ask, how much money does Ahmad save (or lose) by choosing purchasing plan A rather than purchasing plan B?
Ah, buying in bulk. How many other exams teach economy of scale? (A genuine question.)
Post a Comment